データベーススペシャリスト資格｜2022年10月挑戦ログ　6月5日｜SQL（関数の確認ドリル）｜統計の基礎⑦ （検定）

この記事は「データベーススペシャリスト資格に興味はあるが、どのようなものか？どう学ぶのか？」という方向けに、具体的な内容と私自身の挑戦ログをお伝えする。学び中の方や、これから学ぼうとされる方の参考になれば幸いだ。

今回は「関数の確認ドリル」について書く。なお、SQL（データ分析）はあくまで目的を達成するための手段だ。例えば売り上げ増加を目的に、顧客の購入歴から筋の良い商品をSQLを使って分析するなどだ。このように「目的に沿ってデータを集め、整理、比較、分析、仮説検証する手法」が統計学であり、意味のあるデータ分析に欠かせない要素だ。よって目的を見失わないようにするため、今回から複数回に分けて統計学の基礎をおさらいする。（統計については、今回が一旦最終回となる）

※注意点として、SQLはDBMSによって作法が異なる。この記事はGoogle Big Queryに準拠するものであることをお含みおき願いたい。

問題021（SQL 関数の確認ドリル）
統計の基礎⑦（検定）
考察
考察のシンプル化と英訳（練習中）
参考書籍

問題021（SQL 関数の確認ドリル）

前回振り返り

SQLについて。これまで基礎（基本構文・グループ化・複数テーブル・仮想テーブル）を学び、実際に記述できるようになった。そこで応用としてSQL関数を少しづつ学んでいく。
前回は「統計集計関数」に関して学んだ。以上で基本的な関数は一通り学んだため、今回は「確認ドリル」を解く

問題文

[customers]テーブルの[name]フィールドには、氏名が半角スペース区切りで格納されています。
[name]とは別に、姓を[family_name]、名を[first_name]として取り出してください。
結果テーブルは3カラムになります。
全員分を確認する必要はないので、5名分だけ表示してください。

テーブルの確認

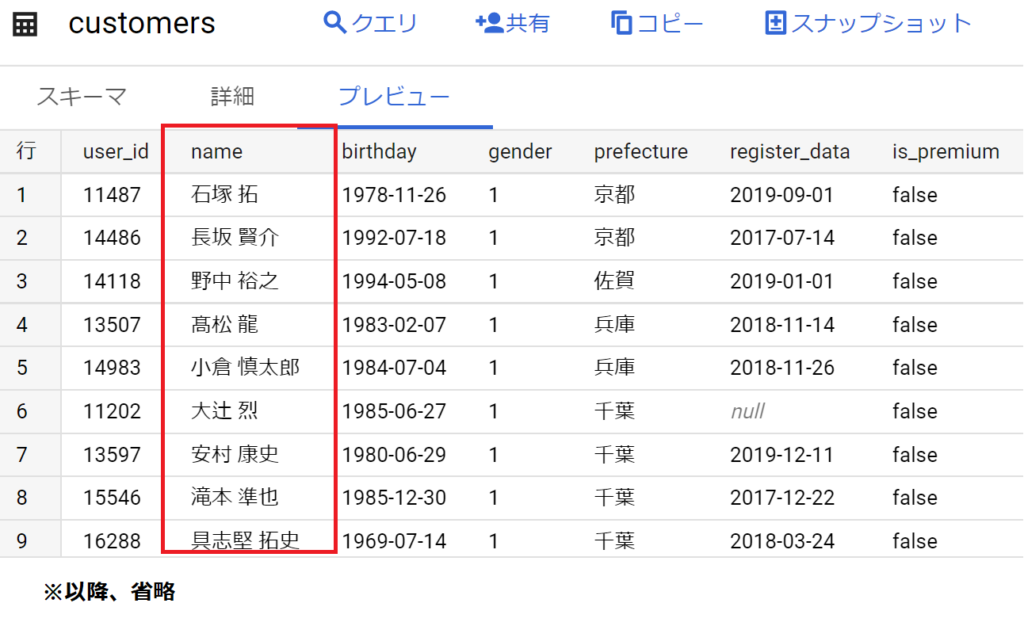
まず、「[customers]テーブルの[name]フィールドには」とあるのでこれを見てみる。
たしかに以下のとおり、氏名が半角スペース区切りで格納されていることが分かる。

姓の抽出（instr関数）

文字列から条件付きで抽出する場合、以前学んだ「instr関数とsubstr関数の組み合わせ」が使える。
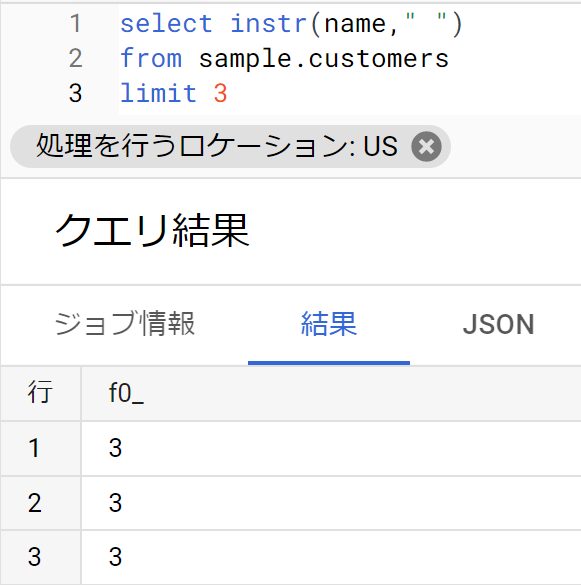
まず、instr関数で「姓と名の間のスペースがどの位置にあるか」を求めてみる。
以下のとおり、たとえば最初の3名なら、3文字目にスペースがあることが分かる。

姓の抽出（substr関数）

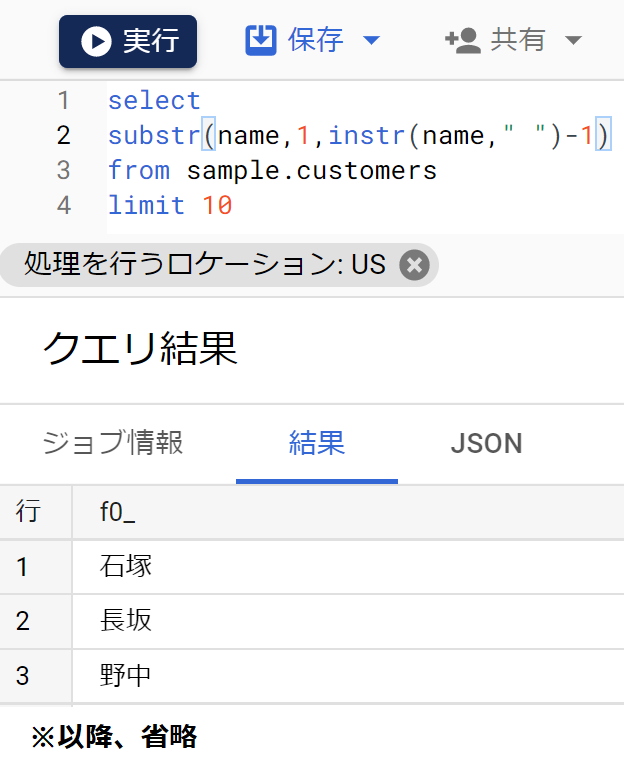
次に、substr関数を使う。引数は「フィールド名、開始位置、抽出文字数」なので
nameフィールドについて、1文字目から、「姓と名の間のスペースがある位置－１」ぶんの文字数を抽出と指定。結果は以下のとおり

名の抽出（instr関数とsubstr関数）

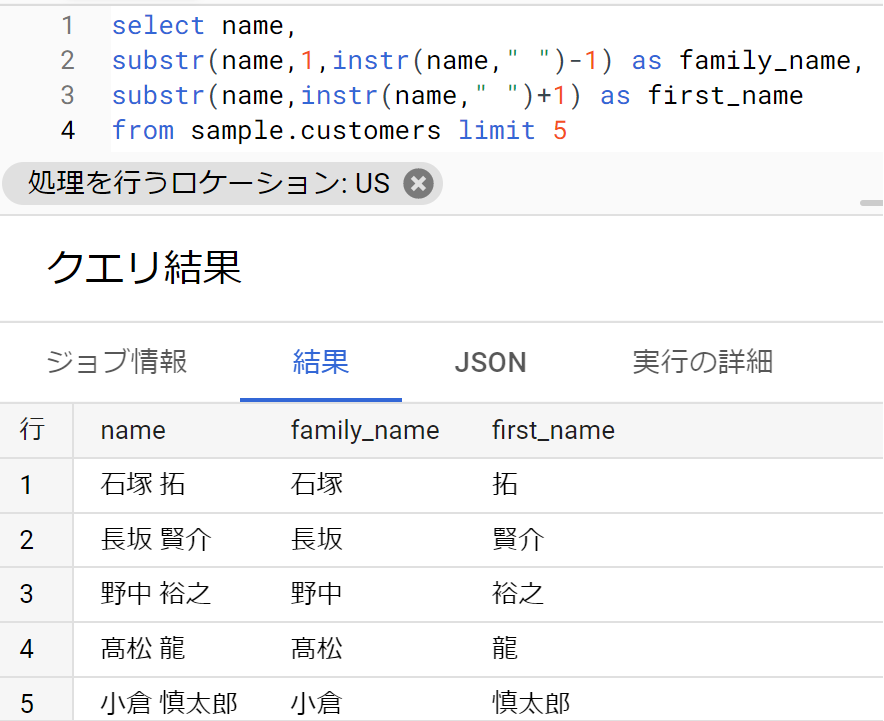
同様に、名についても抽出する。こちらは抽出する開始位置を「姓と名の間のスペースがある位置＋1」にして、抽出文字数指定なし（末尾まで）とすれば良い。
結果は以下のようになる。

統計の基礎⑦（検定）

今までのおさらい（再掲）

書籍「意味がわかる統計学」に沿って、難しい数式を使わず、確率変数を飛ばして、検定・推定のエッセンスを理解したい。
まず、相対度数分布グラフは本書独自の概念。横軸に階級（区切り。中央が階級値）、縦軸に度数（各々の値）のグラフを作り、度数の総計が１になるよう圧縮（相対度数と呼ぶ）したもの。
次に、本グラフにおいて平均は「つり合いが取れるポイント」であり、値は「（階級値×相対度数）の合計」。分散は「平均から見たデータのばらつき具合」であり、値は「（（階級値－平均）の二乗）×相対度数）の合計」。標準偏差は分散の平方根。
ここで重要なのは、相対度数分布グラフがあれば、平均・分散・標準偏差が求められるということ
そして、データ全体について「平均分を引き算し、標準偏差で割る」ことで、平均０かつ標準偏差１にすることを標準化と呼ぶ。これが正規分布（釣鐘状）のとき、この形は最も汎用的に使える重要なひな形。
たとえば標準化されたグラフにおいては、「中心から両翼1.96の位置が全体の95%を占める」。これを利用して前回は推定の考え方を学んだ。（イメージ図は以下のとおり）

検定

検定とは「ある仮説について確からしさを確認すること」。つまり不確かな仮説の大まかな確認。
たとえば、20人からなるAクラスがあったとして、テスト結果は以下のとおりだったとする。
（20人のテスト結果）43,47,52,52,54,61,67,67,68,69,70,71,71,73,76,78,82,84,84,91
このとき、テスト結果が98点の人がいたとして「別のクラスの人じゃないの？（仮説）⇒もしこの人がAクラスだとしたら（仮説の反対）⇒少し点数が高すぎるもの」と考えたとする。
まず、Aクラスの20人のテスト結果の平均は69点、標準偏差13点である。（計算法は前回記事）
次に、98点の人がAクラスだとしたら、標準化された分布のどこに位置するか見る。98点から「平均を引き、標準偏差で割る（標準化）」ので（98-69）/13＝約2.23
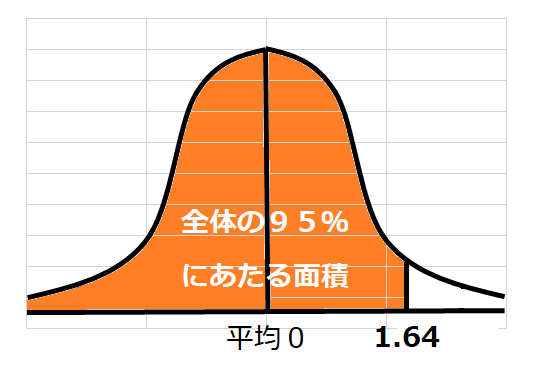
最後に、「平均0、標準偏差1のグラフにおいては、中心から片翼1.64の位置が全体の95%を占める」ことを利用する。イメージは以下のとおり。約2.23は1.64より大きく外れている（イメージ図の白色部分）ので、Aクラスに属さない可能性が高いと予測できる。
よって「Aクラスにしては点数が高すぎるので、別のクラスの人だと考えられる」となる。

これ以上の応用について

7回にわけて「検定・推定のエッセンス」を学んできた。
今まではグラフが正規分布（釣鐘状）の前提だったが、もちろんこれ以外の形もあり得る。例えば初級の検定ならt分布、x^2分布、F分布など。これらの分布は式や具体的な形が表にまとめられているので、考え方・手順は正規分布の時と同じ。
これらを用いれば、「標準偏差がわかっているとき、平均を検定」「標準偏差がわからないとき、平均を検定」「平均がわかっているとき、標準偏差を検定」「平均がわからないとき、標準偏差を検定」などの色々な状況に対応できる。
また、2つ以上のグループ間における平均・分散の比較も行える。これによりたとえば「ある薬を試したグループAと、試さなかったグループBの比較」などが可能になる。
今回の目的は「検定・推定のエッセンスを学ぶ」ことなので、一旦はここまでで終了とする。上記の応用は「意味がわかる統計学」の第2章以降でエッセンスが触れられているので、機会を見て学び直すこととする。

考察

SQLについて。基本的なSQL関数について学習完了した。今回は「関数についての確認ドリル」を解いた。
考察。書籍「意味がわかる統計学/石井俊全/ベレ出版」を元に「検定・推定が何をしているか」を学び直した。今回は今までの学びを振り返り（相対度数分布グラフ、平均・分散・標準偏差、標準化、推定）、それらを用いて「検定が何をしているか」について学んだ。