この記事は「データベーススペシャリスト資格に興味はあるが、どのようなものか?どう学ぶのか?」という方向けに、具体的な内容と私自身の挑戦ログをお伝えする。学び中の方や、これから学ぼうとされる方の参考になれば幸いだ。
今回は「日付・時刻を扱う関数」について書く。なお、SQL(データ分析)はあくまで目的を達成するための手段だ。例えば売り上げ増加を目的に、顧客の購入歴から筋の良い商品をSQLを使って分析するなどだ。このように「目的に沿ってデータを集め、整理、比較、分析、仮説検証する手法」が統計学であり、意味のあるデータ分析に欠かせない要素だ。よって目的を見失わないようにするため、複数回に分けて統計学の基礎をおさらいする。
※注意点として、SQLはDBMSによって作法が異なる。この記事はGoogle Big Queryに準拠するものであることをお含みおき願いたい。
SQL(日付・時刻を扱う関数)
前回振り返り
- SQLについて。これまで基礎(基本構文・グループ化・複数テーブル・仮想テーブル)を学び、実際に記述できるようになった。そこで応用としてSQL関数を少しづつ学んでいく。
- 前回は「正規表現を利用する関数」に関して学んだ。今回は「日付・時刻を扱う関数」について書く
現在の日付・時刻を取得・操作
- 現在の日付・時刻を取得するにはcurrent_date関数およびcurrent_datetime関数
- 引数は「”タイムゾーン表記”」。例えば日本での日付・時刻なら「”Asia/Tokyo”」
- 語源は「current(現在)」および「date(時刻)」と「datetime(日時)」
- 日付、時刻を操作するにはdate_add関数およびdatetime_add関数
- 引数は「date型の値,interval 加える整数 パート」。intervalは定型句。整数はマイナスも指定可能。パートには対象キーワードを指定する。日を加えるならday、月を加えるならweek、年を加えるならyear
- 以下のSQLは現在の日時を取得し、1時間後、1カ月後、1年後を取得するもの

日付・時刻の差分を取得
- さて、現場で日時を扱うシーンの一つ目に、基準間の差異取得がある。たとえば「現在から見て、過去の最終購入日からどれくらい経ったか」を調べるなど
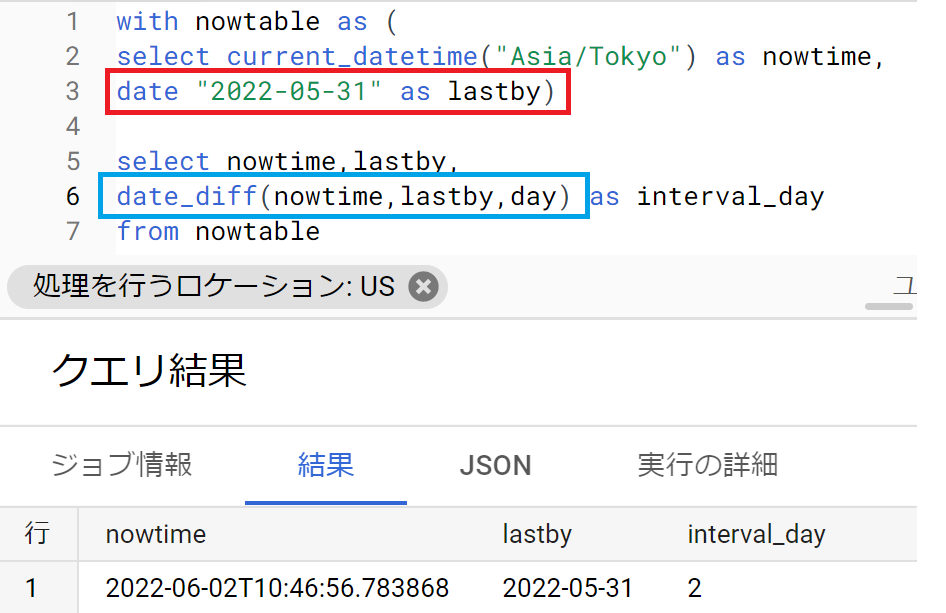
- まず、”現在”の取得は先ほど学んだ。なお基準に固定値を設定したいときはdate関数を使う。たとえば「select date “2022-05-31″」とすれば文字列でなくdate型として認識される。(以下、赤枠)
- 次に、日付・時刻の差分を取得するにはdate_diff関数とdatetime_diff関数を使う。
- 引数は「date型の新しい日付、date型の古い日付,パート」。パートの使い方はdate_add関数と同様。(以下、青枠)
- 語源は「difference(違い)」
- 以下のSQLは、現在から見て、最終購入日”2022-05-31″から何日経過しているかを取得するもの
日付・時刻を丸める、抽出する
- さて、現場で日時を扱うシーンの二つ目に、データ分析の切り口に使用がある。たとえば大量の販売テーブルがあったとき、「月あたりで束ねるとどうか」「月を跨った、同一日で束ねるとどうか」を見るなど。
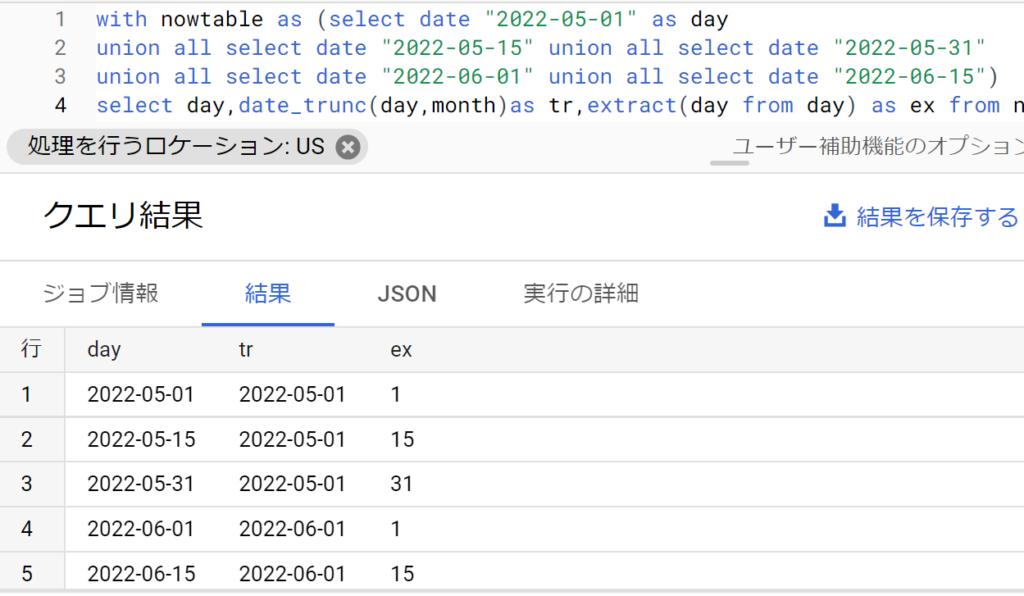
- 日付・時刻を丸める関数はdate_trunc関数とdatetime_trunc関数。引数は「date型の値、パート」。語源は「truncate(切り捨てる)」
- 日付の属性を取得する関数はextract関数。引数は「日付の属性 from date型の値」。語源は「extract(抽出する)」
- 以下は、5つの日付(day)について、月あたりの切り捨て(tr)と、日付の抽出(ex)をしたもの。これらを利用すれば、月単位集計や、月を跨っての同一日集計ができることがわかる。
日付・時刻に関するその他
- Big Queryの場合、日付・時刻の表示形式を指定できる。format_date関数およびformat_datetime関数を使う。これは将来確認ドリルなどで使った際に追記する。
- 日時の増減は算術演算子でも代替可能
統計の基礎⑤(標準化)
相対度数分布グラフ(一部再掲)
- 書籍「意味がわかる統計学」第1章の独自の概念。確率変数を飛ばして、検定・推定のエッセンスを理解できる。「とにかく早く検定・推定で何をしているのか概念だけ知りたい」場合に便利
- 考え方はとてもシンプル。まず横軸に階級(区切り)、縦軸に度数(各々の値)のグラフを作る。これをヒストグラムと言う。
- 次に、度数の総計が1になるよう全体を圧縮する。これが相対度数分布グラフ。
平均と分散(再掲)
- 平均は「データの合計÷データの数量」で求める。相対度数分布グラフにおいては「ちょうどつり合いが取れるポイント」であり、値は「(階級値×相対度数)の合計」
- 分散は「偏差平方和(平均とデータの差を二乗し、合計して平均を取る)」で求める。相対度数分布グラフにおいては「平均から見たデータのばらつき具合」であり、値は「((階級値-平均)の二乗)×相対度数)の合計」
- 標準偏差は分散の平方根(ルート分散)
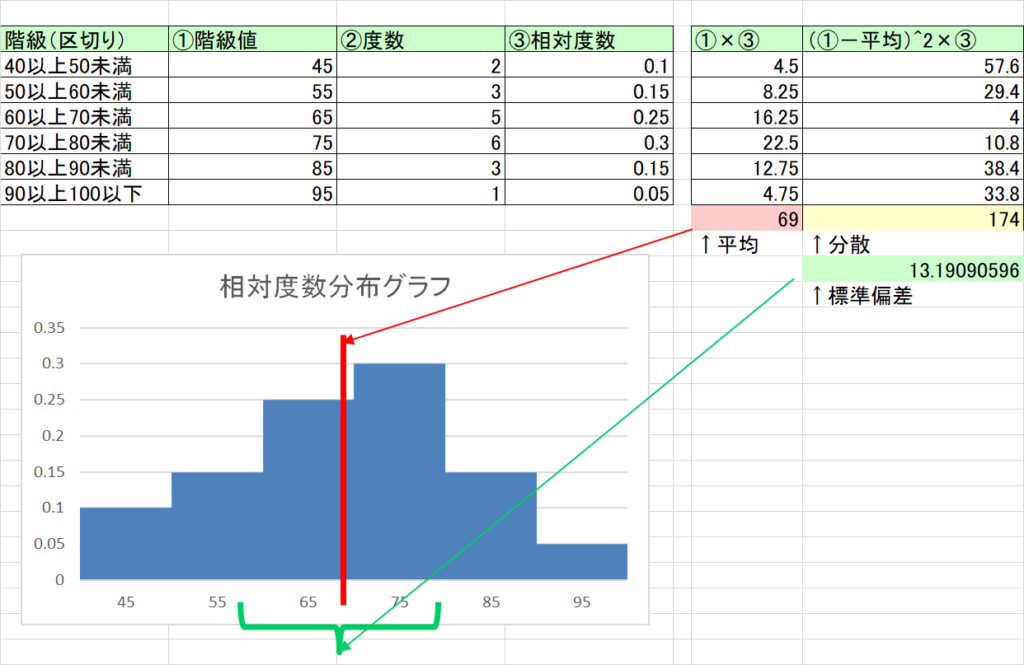
- たとえば20人のテスト結果が以下のとき
- 「43,47,52,52,54,61,67,67,68,69,70,71,71,73,76,78,82,84,84,91」
- 相対度数分布グラフ、平均・分散・標準偏差は以下のとおり
- ここで重要なのは、相対度数分布グラフがあれば、平均・分散・標準偏差が求められるということ
(図1)元のデータ
平均と分散の変化(足し算引き算)
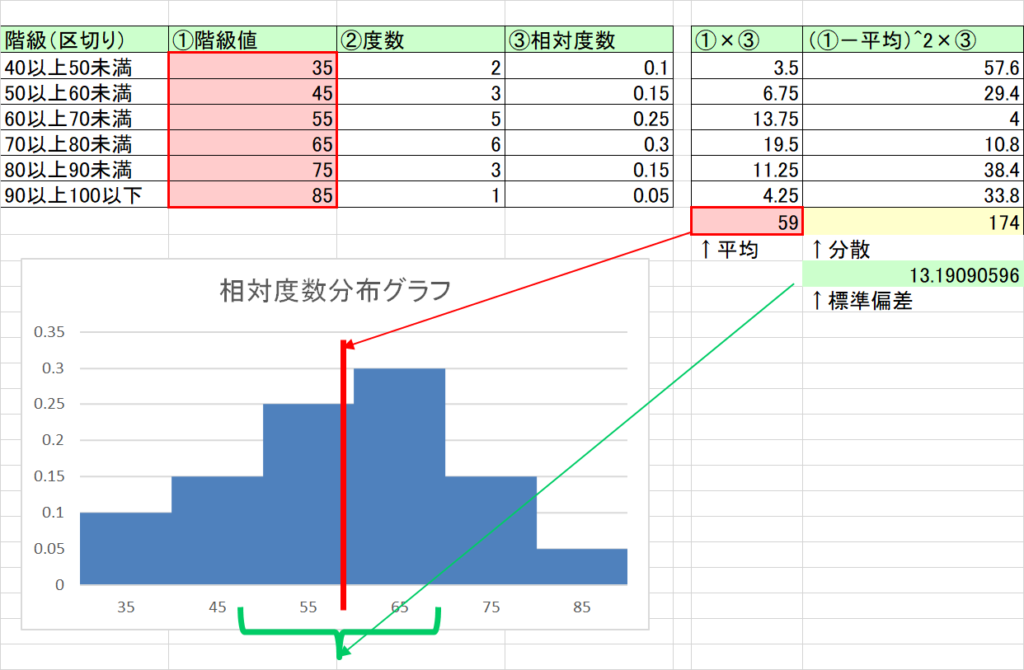
- データ全体に足し算や引き算をすると、平均はその分変化するが、分散(標準偏差)は変わらない。
- たとえば以下は、図1のデータから一律マイナス10点した場合。平均はマイナス10点(69点から59点)になっている(赤枠部分)。
- ただし分散は約174、標準偏差は約13で図1と変わらない。
(図2)一律マイナス10点したデータ
平均と分散の変化(掛け算割り算)
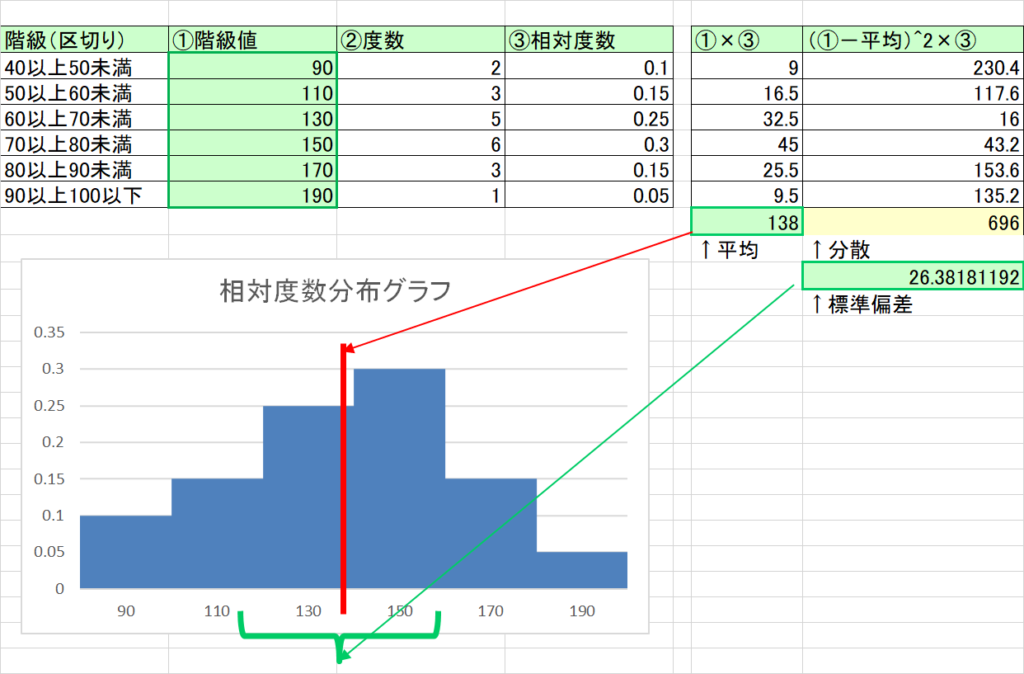
- データ全体に掛け算や割り算をすると、平均も標準偏差もその分変化する。
- たとえば以下は、図1のデータから一律2倍にした場合。平均は2倍(69点から138点)になり、標準偏差は2倍(約13点から約26点)になっている。(緑枠部分)
- なお、分散は標準偏差の2乗なので、元の4倍になっている。(174点から696点)
(図3)一律2倍にしたデータ
標準化
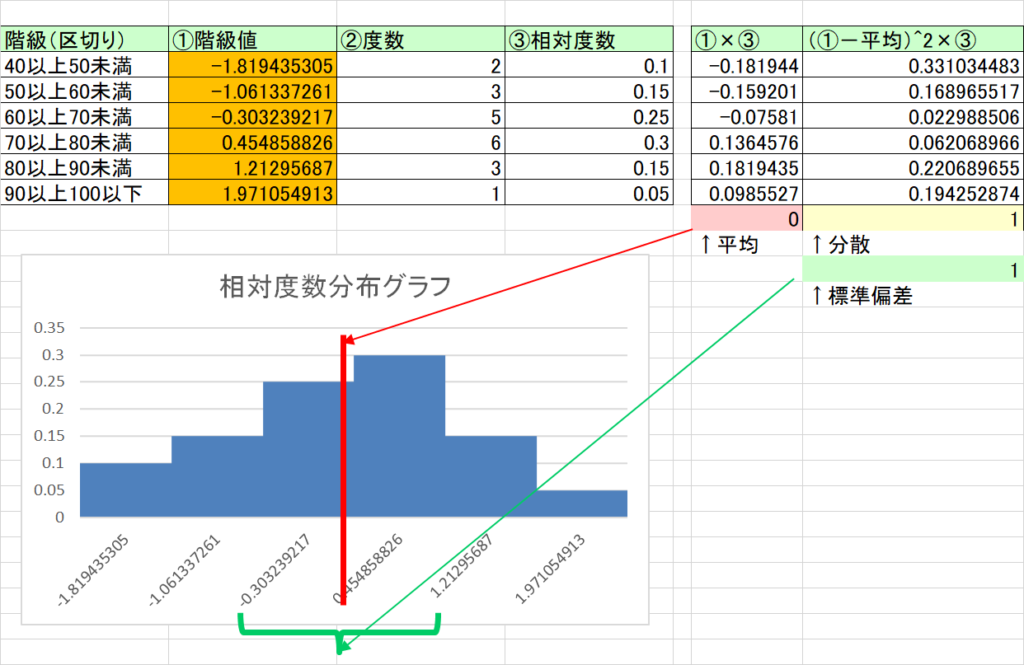
- それでは、データ全体について「平均分を引き算し、標準偏差で割る」とどうなるか。
- まず平均分での引き算により、平均はゼロになる(標準偏差は変わらない)
- 次に標準偏差での割り算により、平均はゼロのまま、標準偏差は1になる。
- このように、データ全体について「平均分を引き算し、標準偏差で割る」ことで、平均0かつ標準偏差1にすることを標準化と呼ぶ。
- なぜ標準化をするか、それはデータの分布が正規形(釣鐘状)であるとき、平均0かつ標準偏差1のこの形が最も汎用的に使える重要なひな形であるから。
- 以下は実際にデータ全体から平均(69点)を引き、標準偏差(約13)で割ったもの。平均が0かつ標準偏差が1になっていることがわかる
(図4)標準化
考察
- SQLについて。応用としてSQL関数を少しづつ学んでいく。今回は「日付・時刻を扱う関数(現在日時を取得、日時間の差異取得、日時の丸めや抽出)」について学んだ。
- 考察。書籍「意味がわかる統計学/石井 俊全/ベレ出版」を元に「検定・推定が何をしているか」を学び直している。今回は本書籍独自の概念である「相対度数分布グラフ」から平均・分散・標準偏差を求めたうえで、それを標準化(平均0、標準偏差1の正規分布に変換)する方法を学んだ。
考察のシンプル化と英訳(練習中)
- I learned standardization in statistics. Because this is useful for assumptions and estimates.
- (私は統計学の中の標準化を学習します。なぜならこれは、仮定や推定に役立つからです)
参考書籍
- 集中演習 SQL入門/木田和廣/株式会社インプレス
- 意味がわかる統計学/石井俊全/ベレ出版


コメント