この記事は「データベーススペシャリスト資格に興味はあるが、どのようなものか?どう学ぶのか?」という方向けに、具体的な内容と私自身の挑戦ログをお伝えする。学び中の方や、これから学ぼうとされる方の参考になれば幸いだ。
今回は「文字列を扱う関数」について書く。なお、SQL(データ分析)はあくまで目的を達成するための手段だ。例えば売り上げ増加を目的に、顧客の購入歴から筋の良い商品をSQLを使って分析するなどだ。このように「目的に沿ってデータを集め、整理、比較、分析、仮説検証する手法」が統計学であり、意味のあるデータ分析に欠かせない要素だ。よって目的を見失わないようにするため、複数回に分けて統計学の基礎をおさらいする。
※注意点として、SQLはDBMSによって作法が異なる。この記事はGoogle Big Queryに準拠するものであることをお含みおき願いたい。
SQL(文字列を扱う関数)
前回振り返り
- SQLについて。これまで基礎(基本構文・グループ化・複数テーブル・仮想テーブル)を学び、実際に記述できるようになった。そこで応用としてSQL関数を少しづつ学んでいく。
- 前回は「数値を扱う関数」に関して学んだ。今回は「文字列を扱う関数」について書く
文字列の連結
- 文字列の連結にはconcat関数(引数としては、連結する文字数を「,」でつないで記述する。テーブルの列名も指定可能。固定文字列は「’」または「”」で囲む)
- 語源は「concatinate(連結)」
- たとえば、テーブルに含まれる氏名に「様」をつけるSQLは以下
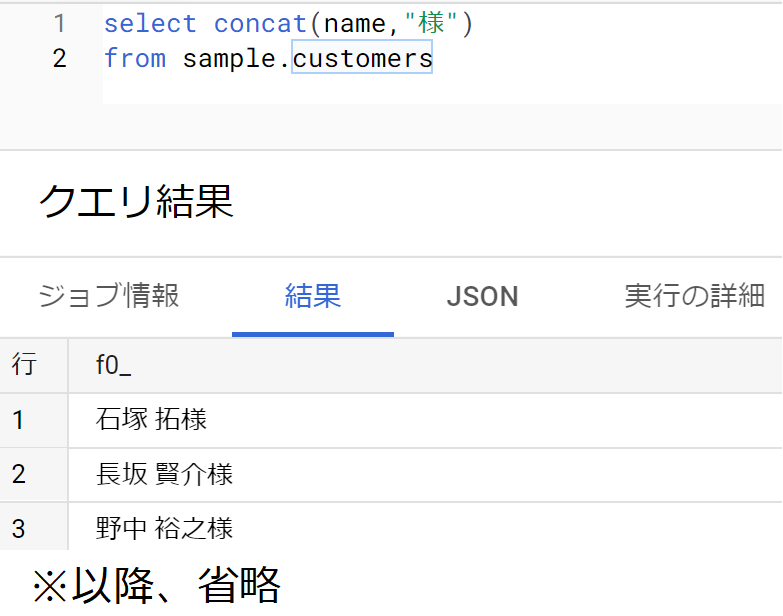
文字列の連結(フィールドの値同士)
- concat関数はフィールドの値同士の連結も可能。
- また、文字列以外のフィールドはBig Queryが自動的に「文字列だとみなして」連結してくれる場合がある。
- たとえば、web_logテーブルにある文字列型のcidフィールドと、数値型のsession_countフィールドを、間に「-」を挟んでつなげるなど。SQLは以下のとおり。
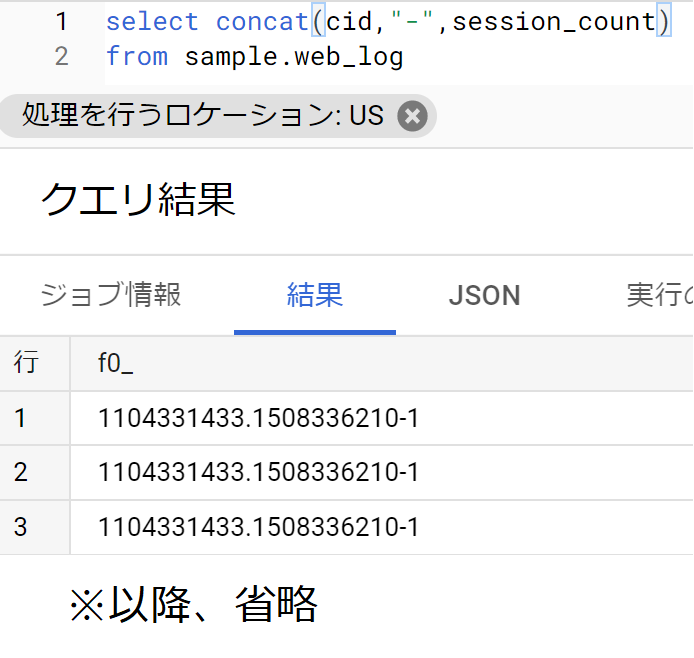
文字列の一部を取り出す
- 文字列の一部取得はsubstr関数。引数には「対象文字列,位置,文字数」を指定する。
- 語源は「substring(部分文字列)」
- 位置はマイナスで入れると、右から数えた場所になる。文字数は省略すると末尾までの文字を取得する。SQLは以下のとおり。
- なお、取得開始位置が左端の場合はleft関数が、右端の場合はright関数が使える。

特定文字列の出現位置を取得する
- 特定文字列の位置取得はinstr関数。引数には「対象文字列,検索文字列,検索開始位置,出現回数」を指定する。後ろ2つはオプション。見つからなかった場合は「0」が返る。
- 語源は(おそらく)「in strings(文字列の中)」
- 以下はサンプル。f1は最初の”晴”が4文字目から出てくるので「4」が返る。
- f2は検索開始位置を5文字目からにしており、f3は出現回数2回目からとしたので、次に”晴”が出てくる「9」が返る。
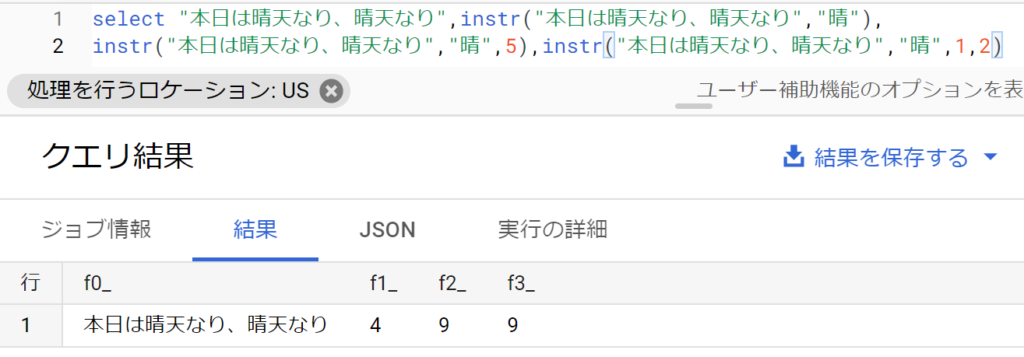
substrとinstr関数の組み合わせ
- たとえば、urlの第一ディレクトリ名のみ抽出、という使い方ができる。
- 以下はSQL。instr関数で第一ディレクトリの開始・修了位置を取り、それをsubstr関数の引数として用いている。
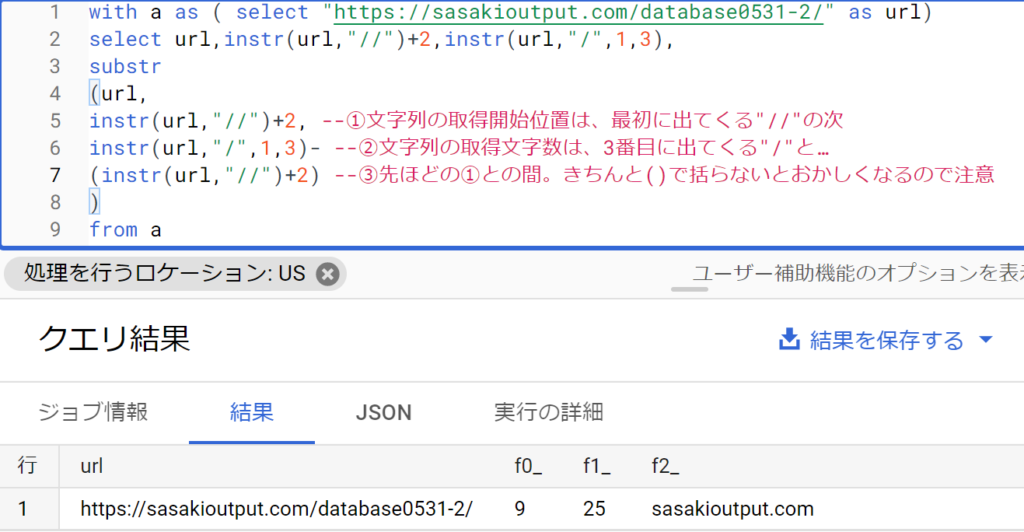
それ以外の関数
- instrの簡易版がstrpos関数。引数では対象文字列と検索文字列しか指定しない。語源は(おそらく)「string position(文字列の位置)」
- 文字列の置き換えがreplace関数。引数は「対象文字列,検索文字列,置換後の文字列」。語源は「replace(交換)」
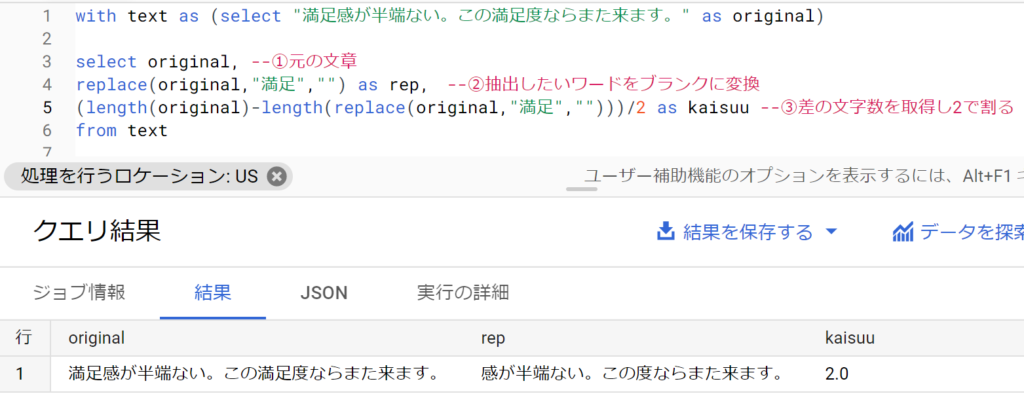
- 文字列の長さ取得がlength関数。語源は「length(長さ)」。replaceとlength関数の組み合わせで、特定文字がどのくらい含まれるか調査できる。以下はSQL。
統計の基礎③(相対度数分布グラフ)
統計を学ぶ理由と注意点(再掲)
- 人間の判断はシンプルに言えば「快か不快か」と「短期は本能、長期は理性」だと思う。たとえば「ドーナツを食べたい(本能的な短期の快)が、太って病気になるのはイヤなので我慢する(理性的な長期の快)」などだ。
- そしてこの「太ると病気になりやすい」などの判断のピースについて、「本当にそうなのか」を明らかにするため、先人の知恵とデータを参考にできるのが統計の強みだと思う。ただし、統計は数学であり、倫理は人が補完する必要があるから、「統計で何ができるか」の学びは重要だと考える。
統計による未来予測(一部再掲)
- データをあつめ、分布をグラフにする。たとえばクラス40人の身長を測り、横軸が階級(何センチ台か)、縦軸が度数(何人いるか)のグラフを作る。これが正規分布(釣鐘状)だったとする。
- 分布から平均と分散をもとめる。平均はグラフの”つり合いが取れる点”。分散は”平均から見たデータのばらけ具合”。平均と分散が分かれば、理想のひな形(平均0、分散1の正規分布)に置換できる。正規分布は重ね合わせしても分布の形が保存されるし、研究されて面積も一覧化されてるのでたいへん便利。
- 検定や推定に用いる。例えば「クラス40人の身長の平均が164センチ、分散が36センチだったとして、身長170センチの人はグラフのどの辺りに属するか?」であったり「クラスA40人とクラスB40人の身長に統計上有意な差はあるか?」などは正規分布を標準ツールとして使うことで求められる。
相対度数分布グラフ
- 書籍「意味がわかる統計学」第1章の独自の概念。確率変数を飛ばして、検定・推定のエッセンスを理解できる。「とにかく早く検定・推定で何をしているのか概念だけ知りたい」場合に便利
- 考え方はとてもシンプル。まず横軸に階級(区切り)、縦軸に度数(各々の値)のグラフを作る。これをヒストグラムと言う。
- 次に、度数の総計が1になるよう全体を圧縮する。これが相対度数分布グラフ。
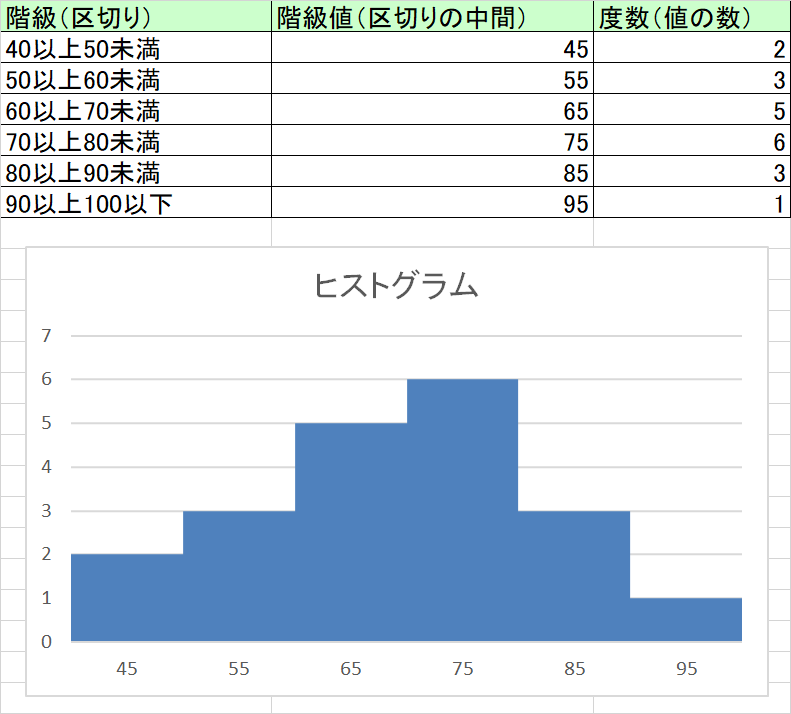
- たとえば20人のテスト点数が「43,47,52,52,54,61,67,67,68,69,70,71,71,73,76,78,82,84,84,91」だったとする。
- このとき、ヒストグラムは以下のとおり。
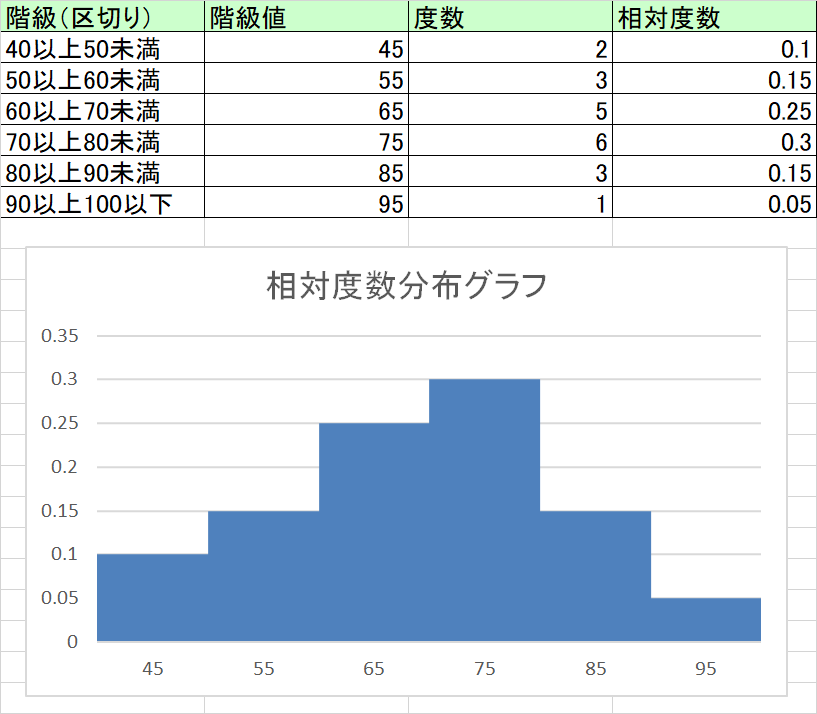
- そして、相対度数分布グラフを作ると、以下の通りとなる。
- なぜ「度数の合計が1」になるよう圧縮するのか。一旦理由は置いておく。ただ一応補足しておくと、「統計は本来確率論で、ある集団からデータを抜き出したとき、それがどのくらいの確率で、どのくらいの値かを計算するものであり、確率の総計は1だから」となる。
考察
- SQLについて。応用としてSQL関数を少しづつ学んでいく。今回は「文字列を扱う関数(結合、抜き出し、位置情報取得、入れ替え、長さ取得)」に関して学んだ。
- 考察。書籍「意味がわかる統計学」を元に「検定・推定が何をしているか」を学び直そうとしている。今回は本書籍独自の概念である「相対度数分布グラフ」を学んだ。確率論や難しい数式を用いず、イメージ図で本質を学べるのは大変ありがたい。
考察のシンプル化と英訳(練習中)
- the introductory book gives me simple learning with graphs. it does not use difficult formula and probability theory.
- (入門書は、グラフを用いてシンプルな学びを私に与えてくれます。難しい公式や確率論は用いません)
参考書籍
- 集中演習 SQL入門/木田和廣/株式会社インプレス
- 意味がわかる統計学/石井俊全/ベレ出版


コメント