データベーススペシャリスト資格｜2022年10月挑戦ログ　5月31日｜SQL（数値を扱う関数）｜統計の基礎②（判断と統計）

この記事は「データベーススペシャリスト資格に興味はあるが、どのようなものか？どう学ぶのか？」という方向けに、具体的な内容と私自身の挑戦ログをお伝えする。学び中の方や、これから学ぼうとされる方の参考になれば幸いだ。

今回は「数値を扱う関数」について書く。なお、SQL（データ分析）はあくまで目的を達成するための手段だ。例えば売り上げ増加を目的に、顧客の購入歴から筋の良い商品をSQLを使って分析するなどだ。このように「目的に沿ってデータを集め、整理、比較、分析、仮説検証する手法」が統計学であり、意味のあるデータ分析に欠かせない要素だ。よって目的を見失わないようにするため、複数回に分けて統計学の基礎をおさらいする。

※注意点として、SQLはDBMSによって作法が異なる。この記事はGoogle Big Queryに準拠するものであることをお含みおき願いたい。

SQL（数値を扱う関数）
統計の基礎②（判断と統計）
考察
考察のシンプル化と英訳（練習中）
参考書籍

SQL（数値を扱う関数）

前回振り返り

SQLについて。これまで基礎（基本構文・グループ化・複数テーブル・仮想テーブル）を学び、実際に記述できるようになった。そこで応用としてSQL関数を少しづつ学んでいく。
前回は「数値の丸め」に関して学んだ。今回は「数値を扱う関数」について書く

絶対値の取得

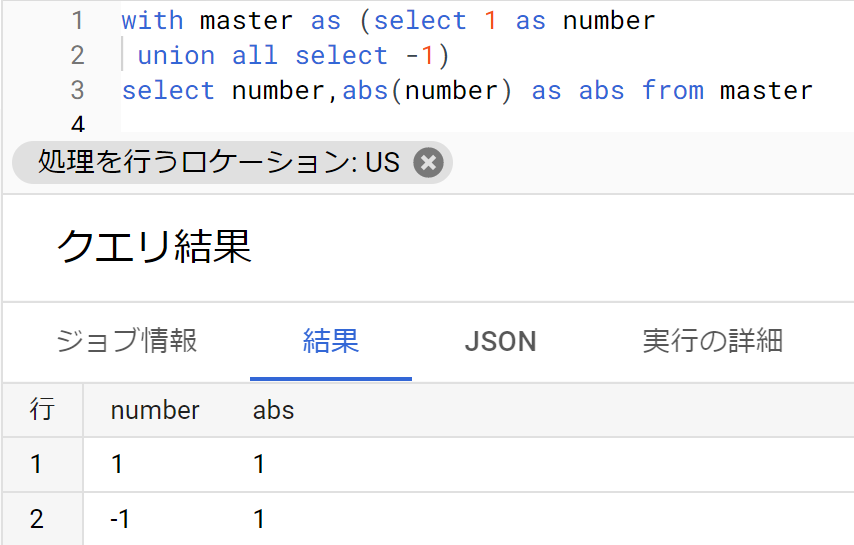
絶対値の取得にはabs関数（abs（フィールド名）で使う）。語源は「absolute value（絶対値）」
SQLの例は以下のとおり。＋も－も絶対値になっていることがわかる。

割り算の余りの取得

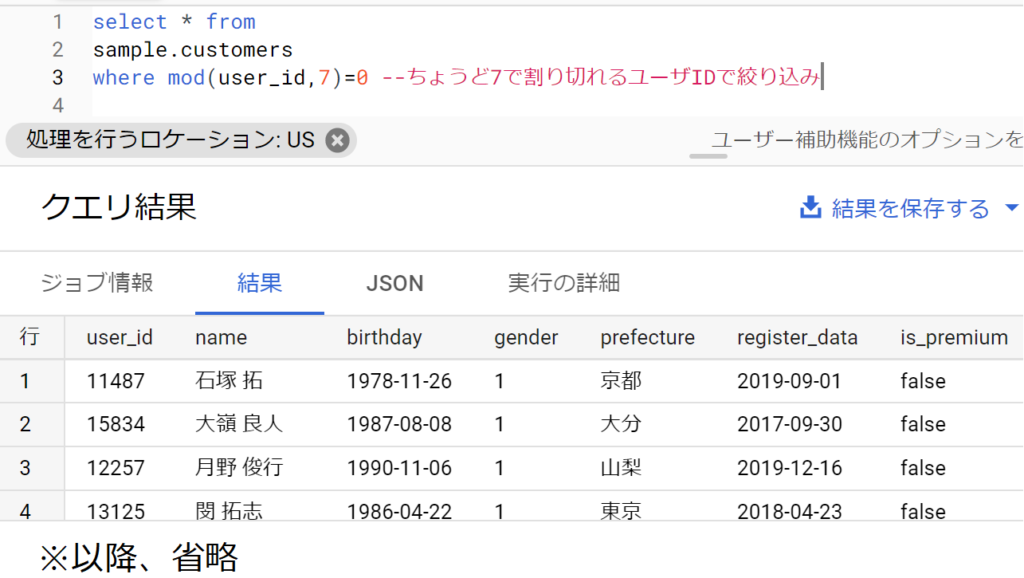
割り算の余りはmod関数。たとえば10を3で割った余りの1が取得できる。語源は「modulus（係数）」
mod（フィールド名,割る値）のように使う。
利用頻度は少ないが、例えば以下のようにサンプリングに使える。

乱数を発生させる

乱数の発生はrand関数。疑似乱数（数学的な厳密さで発生させた乱数ではない）を発生させる。語源は「random（ランダム）」
通常のマーケティングなどの業務における分析には、規則性のないランダムな値として活用できる。
戻り値は「0」以上「1」未満のfloat64型となる。
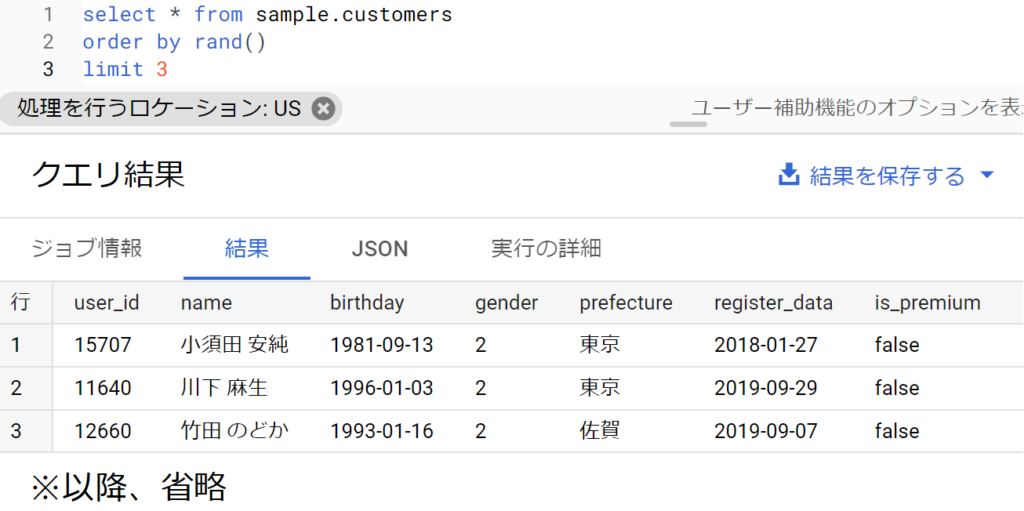
かなり変則的だが、以下のようにしてランダムなユーザーを取得することができる。
本来、order byで指定する値はフィールド名か、列数を表す整数。ただ、結果としてこのような使い方もできると覚えておく。

データ型を変換する

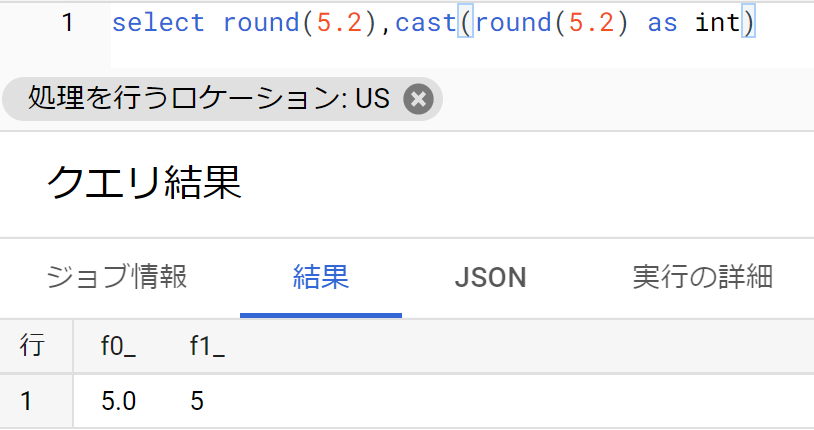
データ型の変換はcast関数。「cast（値 as データ型）」と使う。語源は「cast（型に流し込む）」
たとえば、数値を扱う関数の戻り値は概ねfloat64だが、小数点を含み使いづらいことがある。そこでこれをint（整数）に変換する時などに用いる。
SQLは以下のとおり。

統計の基礎②（判断と統計）

前回のおさらい

さて、前回の記事で「より良い人生を生きるため、自分の頭で大事な判断をするときに、統計が役に立つ」と書いた。
今回はこの点を、もう少し整理して考えてみる。

ふだんどう判断しているか？

私たちは日常生活で、いくつもの判断をしている。たとえば朝食のメニュー、今日着る洋服、傘を持っていくか行かないか…などだ。
この判断はどう行っているか。私は、人が判断をするときは、まず本能が「快か不快か」で選択し、次に（必要に応じて）理性が「その行動は合理的か」で選択するものと考える。
まず、本能は大量の情報を素早く処理し、即座に快か不快かを判断できる。進化の初期にできた能力（脳の辺縁系というエリア）であり、生存には欠かせない。
よって、日常かつささいな判断はかなり本能に頼るところが大きい。たとえば「喉が渇いたとき水を飲む」とき、わざわざ「それが合理的か」などとは考えないだろう。
習慣化が強力と言われるのもここにある。要は「やらないと気持ち悪い」と本能に刷り込むと、継続が苦でなくなるからだ。

理性による判断とは？

次に、理性は限られた情報をゆっくり処理し、合理的かどうか判断する。進化の後のほうにできた能力（脳の前頭前皮質というエリア）であり、いわゆる「人間らしい生き方」には欠かせない。
たとえば本能が「お腹ががすいたからドーナツを食べたい！」と思った時、「いや…太るから我慢しよう。3食で十分だ」と理性がブレーキをかけるイメージだ。
よって、「短期的に見ると不快だが、長期的に見ると快」という判断は理性に頼るところが大きい。
では、理性による判断はどう行っているのか。私は「理性は、長期的に見て快かどうか、論理・確率・統計の３つを用いて判断している」と考える。

論理・確率・統計

ふだん我々が最も使うツールが「論理」だろう。論理とは数学的には「a=b かつ b＝c ならば a=cである」と厳密だが、ふだん使いだともう少しゆるい。
たとえば「甘いものを食べると太る（と言われているし、経験上も間違いない）」⇒「太ると見た目も良くないし病気のリスクが高まる」⇒「健康でいるために甘いものは程々にしておく」といった具合だ。
この「ゆるい論理的判断」は、「数学では扱えない、人間としての倫理的な判断」をも補完するというプラスの側面と、「狭い視野や思い込み、怪しい通説で判断してしまう」というマイナスの側面を持つ。
次に使うツールが「確率」だろう。確率とは数学的には「ランダムに起こる事象について、理論に基づき結果を予測する」ものだが、ふだん使いはもっとゆるい。
たとえば「最後のおやつをどちらが食べるか、じゃんけんで決めよう」⇒「確率的には勝つのは1/2だから、まぁよいだろう」といった具合だ。
では「統計」は判断に使わないのか？そんなことはない。統計は大量のデータから仮説を立て、未来を予測するのに役立つからだ。たとえば「論理」で「太ると病気のリスクが高まる」と考えたが、これは肥満と疾病リスクに相関関係が見られることが統計（検定）で明らかになり、それを我々が学べたからだ。また、日常の「今日傘を持っていくか持っていかないか」の判断では降水確率を調べるが、これも統計のおかげだ（推定）

今後のロードマップ

少しまとめよう。人間は究極「快か不快か」であり、「短期は本能、長期は理性」を使う。
そして「理性は論理と倫理」であり、「統計的に確かな論理」と「原則を抑えた倫理」があればより良い。学びと実践が大事な理由だ。
これから学ぶ統計は、あくまで数学であるし、事象の全てを説明できるわけでも、当然ない。
ただ、大量のデータが手に入り、コンピュータが検定と推定を行う今の時代だからこそ、「どうやって未来予測しているのか？」の仕組みを大まかに把握することが重要だと考える。

統計による未来予測（大まか）

データをあつめ、分布をグラフにする。たとえばクラス40人の身長を測り、横軸が階級（何センチ台か）、縦軸が度数（何人いるか）のグラフを作る。これが正規分布（釣鐘状）だったとする。
分布から平均と分散をもとめる。平均はグラフの”つり合いが取れる点”。分散は”平均から見たデータのばらけ具合”。平均と分散が分かれば、理想のひな形（平均0、分散1の正規分布）に置換できる。正規分布は重ね合わせしても分布の形が保存されるし、研究されて面積も一覧化されてるのでたいへん便利。
検定や推定に用いる。例えば「クラス40人の身長の平均が164センチ、分散が36センチだったとして、身長170センチの人はグラフのどの辺りに属するか？」であったり「クラスA40人とクラスB40人の身長に統計上有意な差はあるか？」などは正規分布を標準ツールとして使うことで求められる。
まずは正規分布で大まかな考え方を理解すれば、他の分布でも応用できる。
また、検定や推定、相関の考え方を理解することで、普段使いで因果推論が可能になる。（その行動は長期的に見て快なのか？その根拠は？）

考察

SQLについて。応用としてSQL関数を少しづつ学んでいく。今回は「数値を扱う関数（絶対値、割り算の余り、乱数の発生、データ型の変換）」に関して学んだ。
考察。人間の判断はシンプルに言えば「快か不快か」と「短期は本能、長期は理性」だと思う。たとえば「ドーナツを食べたい（本能的な短期の快）が、太って病気になるのはイヤなので我慢する（理性的な長期の快）」などだ。
そしてこの「太ると病気になりやすい」などの判断のピースについて、「本当にそうなのか」を明らかにするため、先人の知恵とデータを参考にできるのが統計の強みだと思う。ただし、統計は数学であり、倫理は人が補完する必要があるから、「統計で何ができるか」の学びは重要だと考える。