データベーススペシャリスト資格｜2022年10月挑戦ログ　5月24日｜SQLによるテーマ調査（勤続年数20年は珍しいか｜統計の基礎おさらい

この記事は「データベーススペシャリスト資格に興味はあるが、どのようなものか？どう学ぶのか？」という方向けに、具体的な内容と私自身の挑戦ログをお伝えする。学び中の方や、これから学ぼうとされる方の参考になれば幸いだ。

今回は気分転換も兼ねて、簡単な実テーマを設定し調査してみる。あわせて、統計の基礎のおさらいと、SQLの練習を兼ねる。

※注意点として、SQLはDBMSによって作法が異なる。この記事はGoogle Big Queryに準拠するものであることをお含みおき願いたい。

簡単なテーマ設定
統計の基礎
実データの取得とSQL実践
考察
考察のシンプル化と英訳（練習中）
参考資料

簡単なテーマ設定

私ごとで恐縮だが、私は今の企業に入社しておおむね勤続20年となる。
英会話の練習で海外の先生と会話した際、勤続20年というのは大変驚かれた。海外は雇用の流動性が高いので、さもありなんと納得していた。
日本では普通かと思っていたが、ある先生から「同じ会社で勤続20年以上というのはあまりないですよ」と言われた。
そこで、「日本の企業で勤続20年は珍しいのか」を調査テーマにする。

統計の基礎

統計とは

目的を果たすため、観察・測定し、整理し、指標や図を示すのが統計。
たとえばナイチンゲールの事例。
まず、彼女は兵士の死亡率と死因のデータを集めた。
次に、直接のケガよりも、不衛生による病気の方が問題であることを図で示した。
結果、病院の衛生環境を改善し、多くの命を救った。

平均とは

集団の代表値であり、相対的な比較に便利なのが平均。
計算式は「データの合計÷データ数」
たとえばアドルフ・ケトレーの事例。
まず、彼は綺麗な分布（正規分布）の中央を平均人と呼び、集団の代表値として使えると考えた。
たとえば、体重/身長の二乗が正規分布になるので、中央のBMI 22.5を理想の指標にできるなど。
ただし、平均には多くの欠点があるため、中央値や最頻値などで補う必要がある点は注意だ。

標準偏差とは

平均からの離れ具合であり、珍しい値の特定や仮説検証に便利なのが標準偏差。
計算式は「偏差（各データの平均との差異）平方（二乗）の平均値の、平方根」
正規分布の場合、平均±標準偏差に約68%、平均±標準偏差の2倍に約95%の値が含まれる。
これを利用して、ある値が珍しいかそうでないか見分けられるし、ある仮説が正しいかそうでないか概ね判断できる。

大数の法則と中心極限定理とは

「試行回数が多いサンプル平均は、真の平均に近づく」ことが大数の法則。たとえばコイン投げで表が出る確率は1/2だが、試行回数が多いほど統計値もこれに近づく。
これを応用して「ランダム抽出した十分な数の標本を用いたとき、各標本の平均値を計算してヒストグラムにすると正規分布になる」ことが中心極限定理。
例えばうまい棒は1本あたり概ね約6～8グラムらしい。近所のスーパーにある30本を実際に測って横軸にカテゴリ（1～2グラム、2～3グラム…と1グラム刻み）、縦軸にカテゴリ内に収まる数量を持つグラフ（ヒストグラム）を書くと、おそらく6～7グラムと7～8グラム辺りが最も高い釣鐘型のグラフになるはずだ。これは感覚的にもイメージしやすい。
これを利用して、例えば選挙の投票結果を調べる際、ランダムサンプリングを調査して結果をある程度予測するなどが可能になる。なお、ランダム抽出した標本の確からしさを測る指標に信頼区間がある。（計算にはt分布表等を用いる）

統計の実例と振り返り

統計や分析は、何らかの目的を果たすために行うもの。（ナイチンゲールの事例であれば「一人でも多くの命を救いたい」が目的。以降、カッコ内はこの事例に沿う）
平均は相対的な比較に便利。（年度ごと死亡率の平均を、一般市民と兵士で比べると、明らかに後者の方が多いことを確認。まずは正しい現状認識）
大数の法則や中心極限定理により、ある程度の無作為サンプルがあれば全体を予測できる。（ある程度の兵士の死亡率を確認し、その結果を全体に適用する）
標準偏差は仮説検定に使える。（これはフィクションだが、「不衛生な環境が病気の原因」と仮説を立てたとする。⇒反対の仮説を一旦置く。「衛生環境は病気と関係ない」⇒ランダムに抽出した協力者（標本）を2つのグループに分け不衛生（介入群）と衛生（対照群）に分け、一定期間観察⇒2つのグループの差を確認。例えば不衛生グループの一人にヒアリングし、明らかに衛生グループと比べて体調が優れなさそうとする。そのような人が10人続いたら、さすがに反対の仮説はムリがある（棄却される）⇒結果として仮説は正しそうだと裏付けされる）
計算の補足。ヒアリング内容が「体調が良いか悪いか」の二択なら二項分布を用いて計算できる。二択を10人に聞いてちょうど8人が「悪い」と答える確率はエクセルだと「=BINOM.DIST(8,10,1/2,FALSE)」であり約0.04。

実データの取得とSQL実践

実データの取得

さて、まず日本における勤続年数はどこから取得すればよいのか。
まず慣れていないときは、総務省統計局の「なるほど統計学園」という学習サイトが目当てのデータを探す参考になる。
こちらで「初級＞データの探し方＞基幹統計から探す＞労働・賃金」と進み、キーワード「平均勤続年数」を含む「民間給与実態統計」を選択。
「民間給与実態統計」の下のほうにある「統計表一覧」で目当てを探す。「14表　企業規模別・勤続年数別」を見てみることにする。
同ページの下のほうにある「調査結果＞令和2年分調査」と進み、14表のエクセルをダウンロードする。

SQL実践（テーブルの作成）

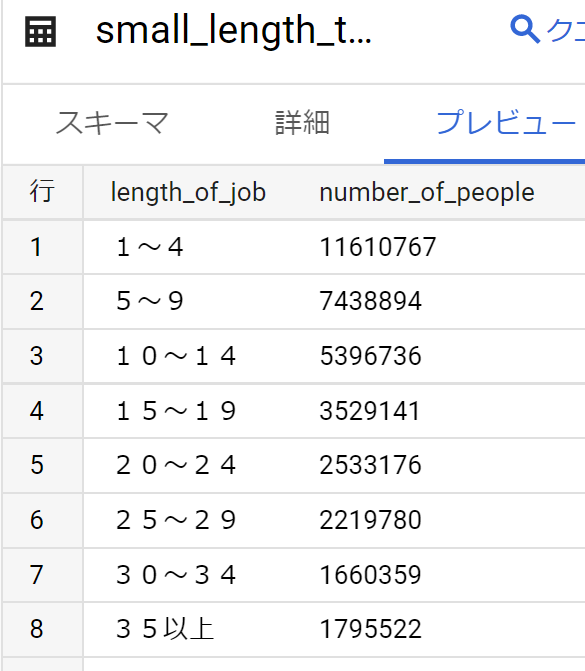
まずはお試しで、第14表その1「給与所得者数」のうち、株式会社の男女総合計の値のみ取得。
エクセルで縦横入れ替えコピーし、勤続年数と人数の以下簡単なテーブルを作成。
なお、エクセルからBig Queryのテーブルを作成する方法はこちら

データの仮分析

さて、今回の目的は「勤続年数20年は珍しいのか」の調査。
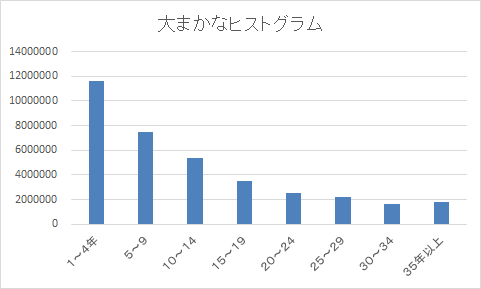
まずヒストグラム（横軸にカテゴリ、縦軸に該当する数）をエクセルで作成すると以下のとおり。
見てのとおり右肩下がりで、釣鐘状の正規分布でない。
よって残念ながら、標準偏差を使った外れ値の分析はできない。

元データの加工

それでは参考値として全体の平均勤続年数を求めたいのだが、今の管理値（１～４年などの範囲値）のままではそれが計算しづらい。（年数別の表があれば良いのだが、今回はお試しなのでこのテーブルを使いたい）
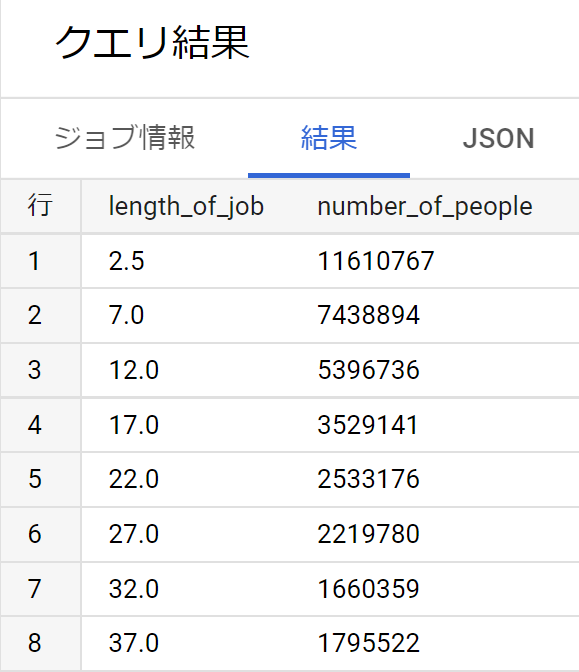
そこで一定誤差が出ることを承知のうえで、範囲値を平均値に置き換える。（例えば勤続年数１～４年なら、平均の２．５年に置き換える。なお、勤続年数35年以上は大卒23歳に入社して定年が60歳と仮定し範囲値35～39年とする）
この操作はデータが少ないためエクセルの方が楽。操作して再度SQLに取り込んだテーブルが以下。（なぜかnullの行列が大量に生成されたので、目当ての行列だけ抽出しなおしてビューで保存）

SQL実践（平均の計算）

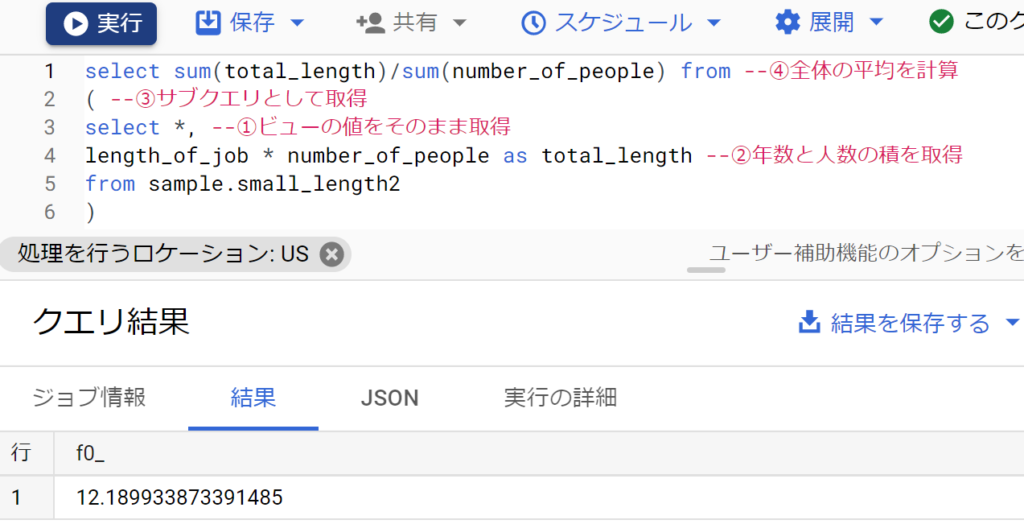
さて、上のテーブルを用いてまずは平均勤続年数を計算してみる。
これは単純に、各カテゴリごとに勤続年数×人数を求め、その平均を取得すればよい。
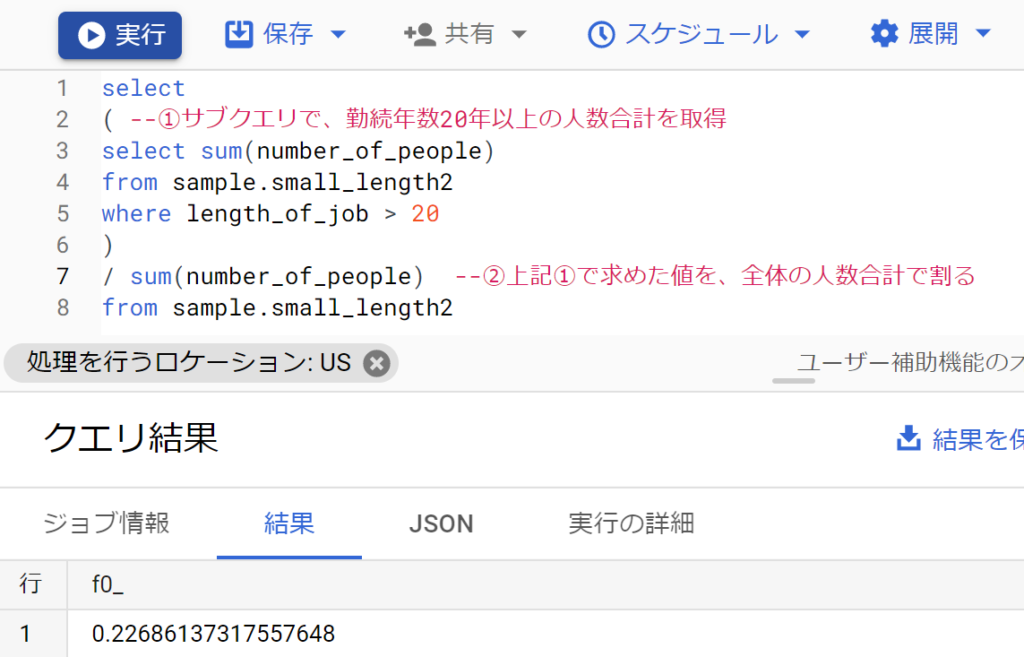
SQLは以下のとおり。一度サブクエリを作り、それを利用し全体の平均を計算している。

結果の妥当性の確認

さて、以上から大まかだが会社勤めの勤続平均年数は約12.2年となった。
これは前述のとおり「民間給与実態統計の令和2年調査結果」を元に、「株式会社（規模不問）の男女総合計の値のみ」を用いて、「勤続35年以上を35～39年に仮置き」しているので本当に大まかな値である。
とはいえ一応、google検索で「勤続年数　平均」で見ると2019年に約12.4年とあるので、大きく外れてはいなさそうだ。

SQLの実践（割合の計算）

さて、このテーブルは非正規分布なので標準偏差は使えない。
そこできわめて単純に、勤続年数20年以上の人数が、全体のうち何％かを計算する。
SQLは以下のとおり。おおむね全体の22%に属すると判明した。

データに関する分析

さて、以上から「日本の株式会社の男女総合計内で見ると、勤続平均年数は約12.2年であり、勤続年数20年以上の割合は約22%である。よって勤続年数20年はやや珍しい部類になる。」ことが分かる。
また、母集団を「株式会社（規模不問）の男女総合計の値」でなく、「①株式会社（規模10億以上）の男女総合計」や「②株式会社（規模10億以上）かつ男性のみの総合計」と変えてみる。
①は平均勤続年数は15年、勤続年数20年以上の割合は約33%、②は平均勤続年数は16年、勤続年数20年以上の割合は約40%となった。
これにより「条件を大企業（規模10億以上）かつ男性で絞ると、勤続平均年数は16年であり、勤続年数20年以上の割合は約40%になるので、勤続年数20年はそこまで珍しくはない。」ことも分かる。

考察

SQLについて。現在は「サブクエリ」について学んでいる。今回は気分転換も兼ねて、簡単な実テーマ（日本の企業で勤続年数20年以上は珍しいか）を設定し調査。あわせて、統計の基礎のおさらいとSQLの練習を兼ねた。
考察。今回は「民間給与実態統計」を元データに、日本の株式会社の男女合計における平均勤続年数（約12.2年）および勤続20年以上の割合（約22%）を、あえてSQLを用いて求めた。そしてテーマについて答えを出した。なお、あくまで練習中かつ初歩の実践ログである点ご容赦願いたい。